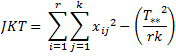ANALISIS VARIANS DUA ARAH - TANPA INTERAKSI (TWO WAY-ANOVA)

Sebelumnya kita sudah membahas mengenai uji analisis ragam satu arah yaitu satu perbedaan kriteria. Biasanya ANOVA digunakan terutama pada rancangan percobaan (Design of Experiment - DOE) yang memiliki implikasi pengambilan keputusan untuk menggunakan teknlogi baru, prosedur-prosedur baru ataupun kebijakan-kebijakan baru. (Nanti kita akan bahas mengenai DOE dan aplikasinya pada MINITAB). 

Sebagai contoh dalam perusahaan industri yang akan merancang produk baru, tentu dibutuhkan beberapa kali percobaan sehingga menghasilkan suatu produk baru yang memiliki kualitas yang baik dn memberikan keuntungan pada perusahaan. Biasanya dalam Six Sigma menggunakan ANOVA untuk DOE. Pada prinsipnya pemakaian ANOVA atau sering disebut uji F yaitu dalam pengujian hipotesis dimana mean dari kelompok bagian sangat berbeda maka variasi kombinasi dari seluruh kelompok jauh lebih besar dari variansi masing-masing kelompok bagian. 

Berikut kita akan lanjutkan analisis ragam dua arah. Pada analisis ragam dua arah yaitu membandingkan perbedaan rata-rata antara kelompok yang telah dibagi dua variabel independen (disebut faktor). ANOVA dua arah terbagi atas dua yaitu ANOVA dua arah dengan interaksi dan ANOVA dua arah tanpa interaksi. pengujian ANOVA dua arah tanpa interaksi merupakan pengujian hipotesis beda tiga rata-rara atau lebih dengan dua faktor yang berpengaruh dan interaksi antara kedua faktor tersebut ditiadakan. Tujuannya adalah untuk menguji apakah ada pengaruh dan berbagai kriteria yang diuji terhadap hasil yang diinginkan. Atau bunyi hipotesisnya adalah tidak ada perbedaan k mean (k>2) pada perlakuan pertama; tidak ada perbedaan k mean (k>2) pada perlakuan kedua; dan tidak ada efek interaksi antara perlakuan pertama dan kedua.

Adapun contoh kasus ANOVA dua arah adalah :

1. Ingin mengetahui pengaruh dari tingkat harga dan tingkat distribusi terhadap keinginan pelanggan membeli barang A (harga : sangat mahal, mahal, murah dan distribusi: sangat lancar, lancar dan tidak lancar).
2. Apakah tingkat pendidikan : bukan sarjana, sarjana muda dan sarjana serta tingkat umur (<35, 35-55, >55) mempengaruhi tingkat konsumsi sejenis minuman tertentu?

Adapun langkah-langkah yang dapat kita lakukan adalah :

1. Uji asumsi data

kenormalan data, independen data dan homoskedastisitas.Sampel berasal dari kelompok yang independen berarti pada saat pengambilan sampel yang dilakukan secara acak terhadap beberapa kelompok dengan nilai suatu kelompok tidak bergantung pada nilai dari kelompok lainnya. Data masing-masing kelompok harus berdistribusi normal dan variansi antar kelompok harus homogen dapat kita uji dengan menggunakan uji kenormalan dan uji homoskedastisitas (akan dibahas pada artikel berikutnya). Jika asumsi tidak dipenuhi maka data harus ditransformasi dan apabila masih tidak memenuhi maka ganti dengan uji nonparametrik. 

2. Membuat tabel pengamatan. Jika kita punya kriteria pertama disebut sebagai blok sebanyak r dan kriteria kedua disebut sebagai perlakuan sebanyak k, maka dapat kita susun tabel sebagai berikut :

Tabel Pengamatan

3. Melakukan perhitungan. Dalam hal ini perhitungan hampir sama dengan ANOVA satu arah.

yaitu menghitung berbagai jumlah kuadrat, yaitu :

JKT = JKB + JKK + JKG

Dimana:

Jumlah Kuadrat Total : 

 Jumlah Kuadrat Kolom

 Jumlah Kuadrat Baris

 Jumlah Kuadrat Galat (error)

4. Merumuskan hipotesis

Dalam ANOVA dua arah terdapat dua kasus yang akan diuji : mean semua perlakuan (kolom) dan mean semua blok (baris).

a. Membandingkan mean semua perlakuan (kolom)

Hipotesis Uji  :

Ho : Semua rata-rata perlakuan (kolom) adalah sama

Ha : Ada rata-rata perlakuan (kolom) yang berbeda

b. Membandingkan mean semua blok (baris)

Hipotesis Uji :

Ho : Semua rata-rata blok (baris) adalah sama

Ha : Ada rata-rata blok (baris) yang berbeda

5. Menentukan taraf signifikansi

Biasanya kita menggunakan alpha 5% yang artinya terdapat sekitar 5 dari 100 peluang bahwa kita akan menolak hipotesis yang seharusnya kita terima atau melakukan kesalahan.

6. Membuat hasil perhitungan ke dalam tabel ANOVA dan menentukan F tabel

Tabel ANOVA

7. Menentukan wilayah kritis atau kriteria pengujian

Daerah kritis disesuaikan dengan F-tabel dan derajat bebas. Untuk menentukan derajat bebas terdiri dari :

• df baris = (r-1)
• df kolom = (k-1)
• df galat = (r-1)(k-1)
• df total = (rk-1)

Mencari F-tabel terbagi atas dua, yaitu :

• Rata-rata baris = F-tabel dengan (alpha; df baris; df galat)
• Rata-rata kolom = F-tabel dengan (alpha; df kolom; df galat)

Mencari wilayah kritis atau daerah pengujian yaitu mencari batas wilayah penolakan Ho atau penerimaan Ho, yaitu :

Ho ditolak jika F-hitung > F-tabel

Wilayah Kritis F

8. Keputusan

9. Membuat kesimpulan 

Kesimpulan disesuaikan dengan hipotesis.

Artikel berikutnya akan kita bahas mengenai contoh ANOVA dua arah tanpa interaksi.

---^_^---

Reference:

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

-Supranto, J. 2004. Analisis Multivariat : Arti dan Interpretasi. Rineka Cipta. Jakarta.

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

PENGENALAN BEBERAPA SOFTWARE STATISTIKA

Dalam memudahkan kita mengolah data dengan analisa statistika, kita dapat menggunakan berbagai macam alat bantu atau software. Adapun software statistika yang dapat digunakan sangatlah banyak namun tidak semuanya memiliki keakuratan yang baik. Ada beberapa software statistika yang sering digunakan baik dalam dunia pendidikan atau pun pekerjaan. 

1. SPSS

Tentu Anda sering mendengar program statistika satu ini, di perkuliahan atau pun di beberapa perusahaan besar pun menggunakan software statistika ini. SPSS singkatan dari Statistical Package for the Social Software. Pertama kali dirilis pada tahun 1968 yang dikembangkan oleh Norman H. Nie dan C. Hadlai Hull. 

SPSS pertama kalo muncul dengan versi PC dengan nama SPSS/PC+ (versi DOS). Setelah mulai populernya sistem WINDOWS maka SPSS berkembang mulai dari versi 6.0 hingga sekarang. SPSS pada awalnya dibuat untuk keperluan pengolahan data statistik untuk ilmu-ilmu sosial (sesuai dengan singkatan dari SPSS itu sendiri).

SPSS pada tanggal 28 Juli 2009 disebut sebagai PASW (Predictive Analytics SoftWare), karena perusahaan ini telah dibeli oleh perusahaan IBM dengan harga US$ 1,2 milyar. Dan pada Januari 2010 menjadi SPSS : Sebuah Perusahaan IBM", dan menjadi nama IBM SPSS yang sepenuhnya diintegrasikan ke dalam IBM Corporation dan merupakan salah satu merk dibawah IBM Software Group Portofolio Bisnis Analytics bersama dengan IBM Cognos.
Untuk mengetahui banyak mengenai IBM SPSS silahkan kunjungi disini.

(Sumber : http://en.wikipedia.org/wiki/SPSS).

2. MINITAB

Software statistika berikutnya adalah MINITAB yaitu program komputer yang dirancang untuk melakukan pengolahan statistik. Minitab menggabungkan kemudahan penggunaan layaknya Microsoft Excel dengan kemampuannya melakukan analisis statistik yang kompleks. 

Minitab dikembangkan di Pennsylvania State University oleh periset Barbara F. Ryan, Thomas A. Ryan, Jr., dan Brian L. Joiner pada tahun 1972. Minitab didistribusikan oleh Minitab Inc, sebuah perusahaan swasta yang bermarkas di State College, Pensylvania dengan kantor cabang Coventry, Inggris (Minitab Ltd) Paris, Perancis (Minitab SARL) dan Sydney, Australia (Minitab Pty.).

Minitab seringkali digunakan dalam perusahaan industri sebagai implementasi Six Sigma - TQM, CMMI serta metode perbaikan proses yang berbasis statistik lainnya dikenal dengan Design of Experiment (DOE). Minitab Inc, juga membuat perangkat lunak sebagai pelengkap Minitab 16, Quality Trainer dan Quality Companion 3.

Jika ingin tahu lebih banyak mengenai MINITAB silahkan klik di sini.

3. SAS

SAS adalah singkatan dari Statistical Analysis System yang disediakan oleh SAS Institute Inc. SAS pertama kali dikembangkan oleh Anthony J. Barr pada tahun 1966. Seorang mahasiswa lulusan dari North Carolina State University lulus 1962-1964.
SAS menggunakan bahasa pemograman, dan memungkinkan programmer melakukan entri data, analisis statistik, peramalan untuk mendukung keputusan riset operasi, peningkatan kualitas pengembangan aplikasi data dan lain sebagainya. Pemograman dalam SAS dikategorikan dalam 2 jenis, yaitu data step untuk membuat, membaca atau pun memanipulasi data, dan proc step (procedure step) digunakan untuk menganalisa, meringkas atau pun membuat tabulasi dari sebuah data. SAS dibangun sejak versi 6.0 hingga versi 9.2. 

Adapun analisa yang dapat dilakukan dengan menggunakan SAS adalah :
1. Base SAS - Basic Procedure and Data Management
2. SAS/STAT - Statistical Analysis
3. SAS/GRAPH - Graphic and presentation
4. SAS/OR - Operation research
5. SAS/ETS - Econometric and Time Series
6. SAS/IML - Interactive matrix language
7. SAS/AF - Aplication facility
8. SAS/QC - Quality control
9. SAS/INSIGHT - Data mining
10. SAS/PH - Clinical trial analysis
11. Enterprise Miner - Data mining

Untuk mengetahui banyak mengenai SAS silahkan kunjungi http://en.wikipedia.org/wiki/SAS_(software)

4. LISREL
LISREL adalah software statistik yang ketiga dan paling sering digunakan dalam dunia pendidikan. Singkatan dari LISREL adalah Linear Structural Relationship. Pada awalnya dikembangkan oleh Karl Joreskog (1973) yang merupakan sebuah nama model persamaan struktural. Dan selanjutnya dikembangkan software komputer yang mendukungnya oleh Joreskog dan Sorbom. Pertama kali software yang tersedia untuk umum adalah LISREL versi 3 tahun 1975. Dan sekarang sudah mencapai LISREL 8.8.
LISREL salah satu software yang digunakan untuk program SEM (Structural Equation Model) yang saat ini masih tercanggih dan dapat mengestimasi berbagai masalah SEM yang bahkan mungkin tidak dapat dilakukan oleh software lainnya. 
Pada edisi terakhir for windows, LISREL memiliki aplikasi statistik sebagai berikut :
1. LISREL untuk SEM
2. PRELIS untuk manipulasi data dan Analisis statistika dasar
3. MULTILEV untuk hierarchical Linear dan Model nonlinear.
4. SURVEYGLIM untuk  GLM (Generalized Linear Modelling).
5. CATFIRM untuk formative inference based recursive modelling for categorical response variables.
6. CONFIRM untuk formative inference based recursive modelling for continuous response variables.
7. MAPGLIM untuk GLM for multilevel data. 

Jika ingin mengetahui LISREL dan mendownload LISREL versi student silahkan kunjungi di sini.

5. AMOS

AMOS adalah singkatan dari Analysis of Moment Structure merupakan salah satu software yang digunakan untuk mengestimasi model pada model SEM. AMOS mengimplementasikan pendekatan yang umum untuk analisa data pada model persamaan struktural yang menjelaskan analisa struktur kovarians, atau causal modelling. Pendekatan ini meliputi kasus khusus banyak teknik konvensional terkenal mencakup model linier yang umum dan analisis faktor umum. 

AMOS memberikan kemudahan dalam proses perhitungan dan analisis menjadi lebih sederhana bahkan orang-orang awam bukan ahli statistik akan dapat menggunakan dan memahami dengan mudah. AMOS diambil alih oleh Microsoft untuk disesuaikan dengan versi SPSS saat ini.

Metode-metode dalam AMOS saat ini diantaranya :
1. Maximum Likelihood
2. Unweighted Least Square
3. Generalized Least Square
4. Browne's Asymptotically Distribution - Free Criterion
5. Scale Free Least Square

Jika ingin mengetahui mengenai AMOS lebih banyak silahkan kunjungi di sini atau di sini.. 

6. EVIEWS
EVIEWS singkatan dari Economic Views merupakan perangkat lunak (software) yang banyak digunakan untuk kepentingan analisis data ekonomi dan keuangan. Pada awalnya dikembangkan dan didistribusikan oleh Quantitative Micro Software (QMS). EVIEWS menyajikan perangkat analisis data, regresi dan peramalan (regression and forecasting). EVIEWS dapat memanipulasi data time series. EVIEWS memanfaatkan lingkungan WINDOWS user-friendly dan kegunaan lainnya antara lain analisis data dan evaluasinya, analisis keuangan, peramalan ekonomi makro, simulasi, peramalan penjualan dan analisis biaya.

Untuk mengetahui lebih banyak mengenai EVIEW silahkan kunjungi di sini.

7. R - Software

R adalah software statistik yang bebas (free software) dibawah lisensi GNU (GNU is not unix) General is Public Licence yang menjamin selalu agar R selalu bebas. Lebih tepatnya R bukanlah suatu program statistika, namun sebuah lingkungan pemograman yang banyak digunakan statistisi. R menyediakan penanganan dan penyimpanan data, mendukung banyak operator perhitungan, menyediakan banyak alat untuk analisis data, menampilkan kemampuan graphical yang baik dan merupakan bahasa pemograman langsung yang didasarkan pada bahasa pemograman S yang ditulis oleh Rick Becker, John Chambers, dan Allan Wilks dari AT&T Bell Laboratories. Nama R diambil dari nama depan penulisnya yaitu Ross Ihaka dan Robert Gentlement di Departemen Statistika Universitas Auckland Selandia Baru.
Untuk mengetahui mengenai bahasa pemograman R silahkan kunjungi di sini.

8. STATA

STATA adalah singkatan dari Statistika dan Data yaitu program komputer yang digunakan untuk analisa statistika dan dibuat oleh StataCorp tahun 1985. Dirancang untuk keperluan ekonomi, sosiologi dan epidemiologi dengan berbagai fitur manajemen data, analisis statistika, grafik, simulasi dan pemograman.

Untuk mengetahui lebih banyak mengenai STATA silahkan kunjungi di sini.

Masih banyak software statistika lainnya yang biasa digunakan dalam analisis data. Untuk software bisa didownload versi trialnya. Analisis data yang pernah saya gunakan adalah SPSS, MINITAB, AMOS, EVIEWS dan yang paling sering digunakan adalah SPSS dan MINITAB. 

Read More

CONTOH ONE WAY ANOVA DENGAN JUMLAH N SAMPEL BERBEDA MENGGUNAKAN IBM SPSS 21

Selanjutnya kita coba untuk menggunakan IBM SPSS 21 pada data Nilai Matematika dari Tiga Dosen.
Berikut langkah-langkahnya (sama dengan sebelumnya):

1. Buka IBM SPSS 21
2. Pilih Variabel View dan isikan seperti berikut ini :

2. Input data pada Data View seperti berikut ini: 

3. Klik Analyze --> Compare Means --> One-Way Anova

4. Pindahkan variabel Nilai  pada kolom Dependent List dan variabel Kelas pada kolom Factor, klik OK.

5. Berikut Output yang kita peroleh

Hipotesis Uji:

Ho : Tidak terdapat selisih antara nilai rata-rata yang akan diberika ketiga dosen.

Ha : Terdapat selisih antara nilai rata-rata yang akan diberika ketiga dosen.

Hipotesis statistik :

Ho : m₁ = m₂ = m₃ = ... = m_k

Ha : Sekurang-kurangnya dua nilai tengah tidak sama.

Statistik Uji :

Pilih nilai signifikansi alpha 5%, dan F-tabel dengan df(JKk) =k-1=3-1=2 dan df(JKg) =n-k=40-3=37. Sehingga diperoleh F-tabel =3,25.Dan pada tabel ANOVA kolom F diperoleh F-hitung = 0,465.

Keputusan :

F-hitung < F-tabel, Ho diterima dan Ha ditolak.

Kesimpulan : 

Tidak terdapat perbedaan yang nyata di antara nilai rata-rata yang diberikan oleh ketiga dosen tersebut.

Semoga bermanfaat ^_^...

Silahkan comment and sharing di sini...:)

Reference:

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

CONTOH ONE WAY ANOVA DENGAN JUMLAH N YANG SAMA DENGAN IBM SPSS 21

Nah, berikut kita coba bahas contoh analisa ragam satu jalur dengan jumlah n sampel yang sama antar kelompok.  see Contoh Analisa Ragam Satu Jalur Jumlah Sampel Sama.

1. Buka IBM SPSS 21

2. Pada Variable View ketik seperti di bawah ini :

2. Pada Data View, silahkan input data seperti berikut ini:

3. Klik Analyze --> Compare Mean --> One-Way ANOVA

4. Pindahkan variabel Lama ke kolom Dependent List dan variabel Tablet masukkan ke kolom Factor selanjutnya klik OK.

5. Sehingga diperoleh Output sebagai berikut :

Hipotesis uji :

Ho : Kelima tablet memiliki waktu yang sama dalam mengurangi rasa sakit.

Ha : Terdapat tablet yang tidak memiliki waktu sama dalam mengurangi rasa sakit.

Hipotesis statistik :

Ho : m₁ = m₂ = m₃ = ... = m_k

Ha : Sekurang-kurangnya dua nilai tengah tidak sama.

Statistik Uji :

Pilih nilai signifikansi alpha 5%, dan F-tabel dengan df(JKk) =k-1=5-1=4 dan df(JKg) =n-k=25-5=20. Sehingga diperoleh F-tabel =2,87. 

Atau gunakan MS-Excel dengan ketik =finv(alpha;(k-1);(n-k)) = "finv(0,05;4;20)=2,87".Dan dari tabel output diperoleh nilai F-hitung=6,896 pada kolom F.

Keputusan :

F-hitung=6,896>F-tabel=2,87, sehingga Ho ditolak dan Ha diterima.

Kesimpulan :

Kelima tablet tersebut tidak sama dalam mengurangi rasa sakit.

Reference:

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

ANALISIS VARIANS SATU ARAH (ONE WAY ANOVA)

Analisis ragam satu jalur berarti kita ingin mengetahui apakah ada perbedaan rata-rata yang didasarkan pada satu kriteria tertentu. Ada hal yang harus diperhatikan yaitu tujuannya membandingkan rata-rata antar sampel dan sampel yang digunakan adalah berasal dari sampel yang berbeda.

Misalkan kita memiliki k populasi. Masing-masing populasi diambil sampel sebanyak n. Dan k populasi yang diambil adalah bebas serta berdistribusi normal dengan nilai tengah m₁, m₂, m₃,..., m_k dan ragam atau variansi sama s².

Hipotesis uji berbunyi :

Ho : m₁ = m₂ = m₃ = ... = m_k

Ha : Sekurang-kurangnya dua nilai tengah tidak sama

Misalkan x_ij adalah pengamatan ke-j dari populasi ke-i, maka 

Setiap pengamatan dapat ditulis dalam bentuk berikut ini :

Keterangan:

(Note : sampel diambil dari populasi dan jumlah sampel tidak harus sama antar populasi)

Selanjutnya adalah memeriksa apakah sudah memenuhi asumsi :

1. Normalitas, menguji apakah data tiap kelompok memiliki distribusi normal, dapat dilakukan dengan uji normalitas Kolmogorov Smirnov atau Saphiro Wilk.

2. Homogenitas atau tidak ada Heteroskedastisitas, menguji apakah varian tiap kelompok sama dengan uji Bartlet atau uji Levene. (akan dibahas berikutnya).

3. Saling bebas, apakah data tiap kelompok tidak saling berhubungan.

4. Aditif yaitu saling menjumlahkan berarti data adalah rasio / interval.

Jika keempat asumsi di atas sudah terpenuhi, maka kita bisa gunakan analsis ragam ini.

Selanjutnya adalah menghitung variabilitas dari seluruh sampel yang diambil. 

Keterangan :

JKT = Jumlah Kuadrat Total

JKK = Jumlah Kuadrat untuk nilai tengah Kolom

JKG = Jumlah Kuadrat Galat (error)

Langkah berikutnya adalah menghitung derajat kebebasan untuk masing-masing JKK-JKT-JKG, 

df (JKT) = n-1

df (JKK) = k-1

df (JKG) = n-k

dimana df(JKG) = df(JKT) - df(JKK)

Selanjutnya adalah menghitung variansi antar kelompok :

MSk = KTk = JKK / df(JKK) = JKK/(k-1)

MSg = KTg = JKG / df(JKK) = JKG/(n-k)

Dan selanjutnya adalah menghitung nilai F-hitung, yaitu :

F-hitung = KKk/KTg = MSk/MSg

Gunakan tabel distribusi F untuk menghitung F-tabel sebagai pembanding F-hitung, dengan derajat kebebasan  ke-1 : df1=k-1 dan derajat kebebasan k-2 : df2=n-k. 

Untuk mengambil keputusan maka :

- Ho ditolak jika F-hitung > F-Tabel

- Ho diterima jika F-hitung ≤ F-Tabel

Kurva Distribusi F

Dan terakhir adalah membuat kesimpulan dari hasil analisa di atas.

Berikut contoh dalam penggunaan ANOVA satu jalur :

1. Jumlah sampel sama antar populasi.

Dari 5 tablet sakit kepala yang diberikan kepada 25 orang dicatat berapa lama tablet-tablet tersebut dapat mengurangi rasa sakit. Ke-25 orang itu dibagi secara acak ke dalam 5 kelompok dan masing-masing diberi satu jenis tablet yang berbeda yaitu tablet A, B, C, D dan E. 

Dalam pengujian ini ingin mengetahui apakah kelima tablet tersebut sama lamanya dalam mengurangi rasa sakit.

Hipotesis uji :

Ho : Kelima tablet memiliki waktu yang sama dalam mengurangi rasa sakit.

Ha : Terdapat tablet yang tidak memiliki waktu sama dalam mengurangi rasa sakit.

Hipotesis statistik :

Ho : m₁ = m₂ = m₃ = ... = m_k
Ha : Sekurang-kurangnya dua nilai tengah tidak sama.

Statistik Uji :
Pilih nilai signifikansi alpha 5%, dan F-tabel dengan df(JKk) =k-1=5-1=4 dan df(JKg) =n-k=25-5=20. Sehingga diperoleh F-tabel =2,87. 
Atau gunakan MS-Excel dengan ketik =finv(alpha;(k-1);(n-k)) = finv(0,05;4;20)=2,87.

JKT = 834 – 132²/25 = 834 – 696,960 = 137,040

JKK = (3882/5) – (132²/25) = 776,400 – 696,960 = 79,440

JKG = 137,040 – 79,440 = 57,600

dengan df(JKt) = df(JKk) + df(JKg) = 4 + 20 = 24

MSk = KTk = JKK / df(JKK) = 79,440 / 4 = 19,860

MSg = KTg = JKG / df(JKK) = 57,600 / 20 = 2,880

F-hitung = KKk/KTg = MSk/MSg = 19,860 / 2,880 = 6,896

Keputusan :

F-hitung = 6,896 > F-tabel = 2,87, sehingga Ho ditolak dan Ha diterima.

Kesimpulan :

Lama waktu kelima tablet tersebut tidak sama dalam mengurangi rasa sakit.

2. Jumlah Sampel Berbeda antar Populasi

Tiga kelas kuliah matematika dasar diberikan oleh tiga dosen. Nilai akhirnya tercatat sebagai berikut :

Hipotesis uji :

Ho : Tidak terdapat selisih antara nilai rata-rata yang akan diberika ketiga dosen.

Ha : Terdapat selisih antara nilai rata-rata yang akan diberika ketiga dosen.

Hipotesis statistik :

Ho : m₁ = m₂ = m₃ = ... = m_k
Ha : Sekurang-kurangnya dua nilai tengah tidak sama.

Statistik Uji :
Pilih nilai signifikansi alpha 5%, dan F-tabel dengan df(JKk) =k-1=3-1=2 dan df(JKg) =n-k=40-3=37. Sehingga diperoleh F-tabel =3,25. 
Atau gunakan MS-Excel dengan ketik =finv(alpha;(k-1);(n-k)) = finv(0,05;2;37)=3,25.

JKT = 199462 – (2726²/40) = 199462 – 185776,90 = 13685,10

JKK = ((817²/12)+(1071²/15)+(838²/13)) – (2726²/40) =  9667489/12 + 1147041/15 + 702244/13 – 185776,90 = 55624,08+76469,40+54018,77-185776,90 = 186112,25 – 185776,90 = 335,35

JKG = 13685,10-335,35 = 13349,75

dengan df(JKt) = df(JKk) + df(JKg) = 2 + 37 = 39

MSk = KTk = JKK / df(JKK) = 335,35/2 = 167,68

MSg = KTg = JKG / df(JKG) = 13349,75/35 = 381,42

F-hitung = KKk/KTg = MSk/MSg = 167,68 / 381,42 = 0,44

Keputusan :

F-hitung = 0,44 < F-tabel = 3,25, sehingga Ho diterima dan Ha ditolak.

Kesimpulan :

Tidak terdapat perbedaan yang nyata di antara nilai rata-rata yang diberikan oleh ketiga dosen tersebut.

Semoga bernanfaat ^_^...

Silahkan comment and sharing di sini...:)

Reference:

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

ANALISIS OF VARIANCE (ANOVA)

Analisis Of Variance atau dikenal dengan ANOVA atau analisis variansi atau analisis ragam merupakan pengembangan dari uji T. Anova termasuk analisis parametrik sama halnya dengan uji beda mean sebelumnya, sehingga harus memenuhi asumsi agar dalam penafsirannya valid. Adapun asumsi tersebut adalah :

1. Populasi berdistribusi normal

2. Sampel diambil secara acak dan saling bebas

3. Populasi memiliki kesamaan varians (homoskedastisitas).

4. Komponen dalam varians bersifat aditif.

Jadi sebelum dilakukan analisis ragam, hendaklah menguji asumsi apakah terpenuhi atau tidak.

Secara umum, ANOVA menguji dua varians berdasarkan hipotesis nol bahwa kedua varians itu sama. Varians pertama adalah antar sampel (among sample) dan varians kedua adalah varians di dalam masing-masing sampel (within samples). Dalam pengujiannya menggunakan uji-F (perbandingan antara varians antar sampel dengan varians yang ada di dalam sampel) karena digunakan untuk pengujian yang lebih dari dua sampel. 

Terdiri dari tiga jenis uji Anova, yaitu:

1. One Way ANOVA (Analisis ragam satu jalur), didasarkan pada pengamatan satu kriteria.

2. Two Way ANOVA (Analisis ragam dua jalur), didasarkan pada pengamatan dua kriteria.

3. Multi Way ANOVA (Analisis ragam banyak jalur), didasarkan pada pengamatan lebih dari dua kriteria.

Tujuan analisis ragam ini adalah untuk melihat apakah ada pengaruh beberapa kriteria terhadap hasil yang kita inginkan. Biasanya digunakan dalam bidang psikologi, teknik, biologi, kedokteran, dll. 

Dalam hipotesis uji, yang dibandingkan adalah mean atau varians dari pengamatan yang kita teliti.

Adapun contoh kasus yang dapat menggunakan analisis varians, yaitu:

Bila ingin menguji hipotesis ada tidaknya perbedaan secara signifikan antara penghasilan pegawai negeri, petani, pedagang, dan nelayan, maka digunakan ANOVA satu jalur. Dan selanjutnya jika ingin dibandingkan juga apakah ada perbedaan secara signifikan penghasilan antara pegawai negeri, petani, pedagang dan nelayan berdasarkan jenis kelamin, maka digunakan ANOVA dua jalur.

Dalam bentuk tabel dapat kita lihat:

1. One Way ANOVA

Hipotesis ujinya :

Ho : Tidak terdapat perbedaan penghasilan antara pegawai negeri, petani, pedagang dan nelayan.

Ha : Terdapat perbedaan penghasilan antara pegawai negeri, petani, pedagang dan nelayan.

2. Two Way ANOVA

 atau

Hipotesis Ujinya :

Ho. Tidak terdapat perbedaan penghasilan antara pegawai negeri, petani, pedagang dan nelayan berdasarkan gender.

Ha : Terdapat perbedaan penghasilan antara pegawai negeri, petani, pedagang dan nelayan berdasarkan gender.

Langkah-langkah yang dapat dilakukan adalah :

1. Sampel diambil secara acak dan dikelompokkan berdasarkan kriteria tertentu.

2. Memilih metode apa yang paling tepat.

3. Menghitung variability seluruh sampel.

4. Menghitung derajat kebebasan.

Menghitung varians antar sampel dan varians dalam sampel.

5. Menghitung nilai F.

6. Mencari nilai F-tabel pada tabel distribusi F.

7. Membandingkan F dengan F-tabel.

8. Membuat kesimpulan.

Selajutnya akan kita bahas mengenai One-Way ANOVA dan Two Way ANOVA.

Read More