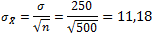PENDUGAAN INTERVAL 2 - CONTOH PARAMETER MEAN

Sebelumnya kita sudah bahas mengenai pendugaan interval, berikut kita akan terapkan pada dua contoh, penerapan interval parameter mean untuk sampel ukuran besar dan sampel ukuan kecil.

Contoh penerapan parameter mean sampel ukuran besar n≥30 dan populasi tidak terbatas.

Suatu lembaga penelitian di Jakarta, mengadakan survei sederhana dengan tujuan utama mengetahui besarnya rata-rata pengeluaran para wisatawan mancanegara yang berkujung ke Bali. Untuk itu diambil sampel acak 500 wisatawan mancanegara yang menginap di beberapa hotel bintang lima di Nusa Dua Bali. Dari survey diperoleh bahwa rata-rata pengeluaran adalah 2.000 dolar per wisatawan untuk setiap kali berkunjung ke Bali yang terdiri atas pengeluaran untuk hotel, transportasi, makan dan barang-barang seni. Bila diketahui simpangan baku pengeluaran untuk semua wisatawan yang berkunjung ke bali adalah 250 dolar, buatlah interval kepercayaan 99% untuk memperkirakan berapa sesungguhnya rata-rata pengeluaran per wisatawan mancanegara untuk setiap kali berkunjung ke Bali?

Kasus di atas adalah pendugaan parameter mean dengan ukuran sampel besar, sehingga dibutuhkan tabel Z.

Jawab :

Jumlah populasi tidak diketahui berarti tidak terbatas (tidak dibutuhkan faktor koreksi untuk menghitung simpangan baku sampel rata-rata)

n = 500  

Rata-rata = 2000

Simpangan baku = 250

Interval kepercayaan = 99%

1 - a = 99% -->  a = 1% = 0,01 --> a/2 = 0,005 -->  Z_a/2 = 2,58

Nilai rata-rata dari sampel rata-rata = 2000

Simpangan baku dari sampel rata-rata = 

Jadi 

Jadi interval kepercayaan 99% untuk memperkirakan berapa sesungguhnya rata-rata pengeluaran per wisatawan mancanegara untuk setiap kali berkunjung ke Bali adalah berkisar antara 1971,16 dolar dan 2028,84 dolar.

Contoh penerapan parameter mean sampel ukuran besar n<30 dan ukuran populasi terbatas.

Suatu sampel acak berukuran 10 mempunyai rata-rata 9,5 dan simpangan baku 3,24. Buatlah interval kepercayaan 90% untuk menduga rata-rata dari populasi tersebut!

Kasus di atas adalah kasus populasi tidak terbatas sehingga tidak dibutuhkan faktor koreksi untuk menghitung simpangan baku sampel rata-rata. Dan ukuran sampel < 30 sehingga digunakan tabel - t.

Jawab :
Jumlah populasi tidak diketahui berarti tidak terbatas (tidak dibutuhkan faktor koreksi untuk menghitung simpangan baku sampel rata-rata)
n = 10  --> df = 10-1=9
Rata-rata = 9,5
Simpangan baku = 3,24
Interval kepercayaan = 90% 
1 - a = 90% -->  a = 10% = 0,01 --> a/2 = 0,05 -->  t(0,05;9) = 1,833
Nilai rata-rata dari sampel rata-rata = 9,5
Simpangan baku dari sampel rata-rata = 8

Jadi

Jadi interval kepercayaan 90% untuk menduga rata-rata dari populasi tersebut adalah berkisar antara 7,63 sampai 11,73.

Jika kasus di atas diketahui jumlah populasinya, maka simpangan baku harus dikalikan dengan faktor koreksi. Yaitu :

contoh sampel besar di atas jika populasi diketahui sejumlah 1000, sehingga simpangan baku seharusnya :

contoh sampel kecil di atas jika populasi diketahui sejumlah 50, sehingga simpangan baku seharusnya :

Dan selanjutnya untuk menghitung interval kepercayaan sama dengan sebelumnya. Hanya saja mengganti nilai simpangan baku yang sudah dikalikan dengan faktor koreksi.

by MEYF ^_^

Read More

PENDUGAAN INTERVAL - 1

Bila nilai parameter q dari populasi diduga dengan memakai beberapa nilai statistik q yang berada dalam suatu interval Õ₁ < q < Õ₂ maka statistik õ disebut Pendugaan Interval. Derajat kepercayaan penduga Õ disebut koefisien kepercayaan yang ditulis dengan a dimana 0 < a < 1 dan dinyatakan dalam bentuk probabilitas.

dimana 

a disebut koefisien kepercayaan
1-a disebut derajat kepercayaan 
P(Õ₁ < q < Õ₂) disebut interval kepercayaan

Terbagi atas dua, yaitu :
1. Pendugaan parameter populasi dengan sampel besar, yaitu n ≥ 30. 
Dalam hal ini statistik q akan memiliki distribusi normal sehingga dapat ditransformasikan ke normal standar. Dan nilai S²  tidak akan terlalu besar perbedaannya dengan sampel lainnya. Sehingga dapat didekati dengan variansi populasi.
Dapat didekati dengan :

Penentuan interval kepercayaan parameter memakai suatu nilai Z_a/2 yang diperoleh dari tabel distribusi normal standar. Berikut beberapa nilai  Z_a/2 yang sering digunakan.

Derajat Kepercayaan	99,73%	99%	98%	96%	95,4%	95%	90%	80%	68,2%	50%
Za/2	3,0	2,8	2,33	2,05	2,00	1,96	1,645	1,28	1,00	0,6745

Berikut cara menentukan nilai Z tabel :

1. Tabel Distribusi Z Model I

Tabel Model 1 untuk nilai yang diarsir adalah nilai dari (0,5 - a).

1. Misalkan kita menggunakan interval kepercayaam 95%.
2. Kita akan menghitung nilai  Z_a/2 berarti ( 0,95 : 2 = 0,475). 
3. Lihat nilai dalam tabel Z yang mendekati 0,475.
4. Diperoleh pada baris 1,9 dan kolom 0,06.
5. Sehingga diperoleh nilai  Z_a/2 = 1,96.

2. Tabel Distribusi Z Model II

Misalkan kita menggunakan interval kepercayaam 95%. Perhitungannya berbeda, Tabel Model II nilai yang diarsir adalah 1 - a, sehingga tidak dibagi dua.

1. Lihat nilai dalam tabel Z yang mendekati 0,95.
2. Diperoleh pada baris 1,9 dan kolom 0,06.
3. Sehingga diperoleh nilai  Z_a/2 = 1,96.

Tentu bisa dicoba untuk nilai Z lainnya.

2. Pendugaan parameter dengan sampel kecil, yaitu n < 30

Dalam hal ini statistik q akan memiliki distribusi normal sehingga dapat ditransformasikan ke normal standar. Penentuan interval kepercayaan parameter mmakai suatu nilai Z_a/2 yang diperoleh dari tabel distribusi normal standar. Berikut beberapa nilai  Z_a/2 yang sering digunakan. Nilai   S²  cukup besar berfluktuasi, sehingga tidak dapat didekati dengan normal standar. Hal ini didekati dengan distribusi Student-T 

Untuk menentukan nilai t-tabel, 

1. Misalkan akan dicari nilai t-tabel untuk a = 0,05 dengan ukuran sampel n=15.
2. Tentukan nilai derajat bebas df = 15 - 1 = 14
3. Lihat baris df=14 dan kolom 0,05, sehingga diperoleh nilai t-tabel = 1,761. 

Tentu bisa dicoba untuk nilai t lainnya.

Berikut perhitungan pendugaan Interval untuk ukuran sampel besar. Sehingga digunakan nilai Z_a/2.

Sedangkan untuk ukuran sampel kecil, maka Z_a/2 ditukar dengan nilai t-tabel atau t(a;df).

Untuk formula di atas digunakan jika ukuran populasi tidak terbatas, sedangkan jika ukuran populasi terbatas makan nilai standar deviasi untuk setiap parameter yang diduga harus dikali dengan faktor koreksi :

by MEYF ^_^

Read More

PENDUGAAN PARAMETER

Statistik inferensia dapat dikelompokkan atas dua yaitu "Pendugaan dan Pengujian Hipotesis". Kita coba ingat lagi beberapa istilah statistik yaitu parameter dan statistik :

Parameter adalah sebarang nilai yang menggambarkan ciri-ciri populasi
Statistik adalah sebarang nilai yang menggambarkan ciri-ciri sampel.

Dalam statistik inferensia yaitu pendugaan adalah ditujukan pada pendugaan parameter populasi, kita menduga karakteristik-karakteristik dari populasi melalui sampel yang diambil dari populasi tersebut.
Parameter ditulis dalam huruf latin dan statistik ditulis dengan huruf biasa dengan memakai tanda topi. Dapat diilustrasikan dalam gambar berikut :

Pendugaan Parameter

Penduga yang baik adalah

1. Tak bias :

2. Efisien : Variansi paling kecil (s² <<<)

3. Konsisten : jumlah sampel besar (n >>>)

Pendugaan parameter terbagi atas dua, yaitu :

1. Pendugaan titik atau tunggal

Bila parameter q dari populasi hanya diduga dengan memakai satu nilai statistik õ (Theta topi) dari sampel yang diambil dari populasi tersebut. Dan õ adalah Pendugaan Titik.

2. Pendugaan Interval atau selang

Bila parameter q dari populasi diduga dengan memakai beberapa nilai statistik õ (Theta topi)  yang berada dalam suatu interval Õ₁ < q < Õ₂ maka statistik õ disebut Pendugaan Interval.

Read More

CARA MENENTUKAN NILAI ALPHA DENGAN MENGGUNAKAN TABEL Z (DISTRIBUSI NORMAL TERSTANDAR)

Masih ingat dengan distribusi normal, yang sebelumnya pernah kita bahas (see Distribusi Normal dan Distribusi Normal Standar). Distribusi normal adalah distribusi kontinu yang biasanya untuk mengukur selang waktu, bobot, tinggi, volume dan lain sebagainya, dan ukuran sampel (n) besar (biasanya n≥30).

Dalam penggunaannya juga berkaitan dengan Tabel Distribusi Normal Standar atau yang dikenal dengan Tabel Z, karena pada Tabel Z menggunakan distribusi normal standar yang selalu memiliki mean nol (m=0) dan standar deviasi satu (s=1) atau biasa ditulis N(0,1). Jika X adalah populasi yang menyebar secara normal dengan mean m dan standar deviasi s maka dapat ditulis X~N(m,s). Jika m=0 dan s=1 maka X~N(0,1).

Pada kurva normal yang berbentuk genta atau lonceng dan simetris serta asimtot terhadap sumbu-X (datar). Pada Kurva Normal Standar atau Kurva Z yang berkaitan dengan Tabel Z, maka ada dua hal terpenting dalam penggunaannya, yaitu taraf signifikansi (nilai alpha, a) dan titik kritis (nilai Z). Taraf signifikansi atau nilai a adalah luas daerah yang berada di bawah kurva normal dan di atas sumbu datar (Sumbu-X), sedangkan titik kritis atau nilai Z adalah titik batas yang membatasi luas daerah tersebut. Coba perhatikan gambar berikut :

Nilai alpha atau luas daerah yang diarsir adalah nilai probabilitas dari variabel X dengan batas titik kritisnya.  Dan jika titik kritisnya dari negatif tak hingga sampai tak hingga, maka luas daerahnya adalah satu. Dan luas daerah dari titik kritis 0 hingga tak hingga sama dengan luas daerah dari negatif tak hingga sampai 0 yaitu 0,5 (karena simaetris, yait 1:2=0,5).

Rumus umum distribusi normal :

dengan 

m = mean

s = standar deviasi/simpangan baku

π = 3,14 = 22/7

e = Eksponensial 

Dan rumus untuk distribusi normal standar (Z) dengan mean nol dan simpangan baku satu :

dengan 

Sedangkan nilai alpha adalah luas daerah di bawah kurva, yang mana kita tahu dalam kalkulus untuk menghitung luas daerah bentuk yang tidak beraturan atau yang diwakili oleh fungsi, adalah menghitung intergral dari fungsi tersebut dengan batas-batas yang diberikan. Khusus untuk gambar di atas dapat kita hitung dengan :

Hal ini nanti akan sangat berguna dalam pengujian hipotesis, untuk memudahkannya menghitung luas daerah di bawah kurva sehingga ada tabel yang memudahkan kita untuk menghitung nilai integral tersebut. Kita kenal dengan Tabel Kurva Normal Standar atau Tabel Kurva Z. 

Mengapa kita menggunakan normal standar ?

Peubah acak yang kita gunakan tidak selalu sama, ada yang berkaitan dengan ukuran berat, panjang, usia, volume, dsb yang mana setiap peubah acak tersebut memiliki nilai peluang (luas daerah di bawah kurva normal yang berbeda-beda) sehingga membutuhkan tabel kurva normal yang berbeda-beda pula. Tentu hal yang membutuhkan waktu yang lama dalam perhitungan jika kita buatkan semua tabel terpisah untuk semua peubah acak. Sehingga dibutuhkanlah standardisasi setiap peubah acak (dalam artian satuan untuk semua peubah akan menjadi sama) menjadi peubah acak normal Z dengan mean nol dan simpangan baku satu. Sehingga kita hanya membutuhkan satu tabel untuk semua peubah acak normal yang berbeda. Dan dalam penggunaannya, setiap peubah acak normal di transformasi kebentuk Z dan selanjutnya gunakan Tabel Z.

Note : Sebaran Normal Baku adalah sebaran normal yang memiliki mean 0 dan standar deviasi satu, dalam hal ini sebaran normal baku adalah sebaran normal standar.

Berikut ada beberapa tabel Z yang penggunaannya berbeda :

1. Tabel Distribusi Z Model 1

Untuk Tabel Z di atas, luas kurva yang diarsir adalah yang berkisar antara nilai Z=0 sampai nilai Z=¥.  Nilai yang ada pada kolom paling kiri dan baris paling atas adalah nilai dari Z=z, dan nilai yang adal dalam tabel (di tengah-tengah) adalah luas daerah di bawah kurva normal antara Z=0 hingga Z=¥.

Contoh 1 :

Contoh 2 :

Untuk melihat Tabel Z dengan nilai 0<Z<1,5 adalah 

• Perhatikan kolom paling kiri dan cari angka 1,5
• Perhatikan baris paling atas dan cari angka 0,00
• Cari angka perpotongan dari baris dan kolom tersebut, sehingga diperoleh nilai 0,4332 (baris ke-16 kolom-1).

Contoh 3 :

yaitu 0,0668

Contoh 4 :

Caranya :

Kurva hanya berkisar antara 0 sampai tak hingga, sehingga untuk titik kritis Z< 0 harus kita cerminkan dan memiliki nilai yang sama di daerah Z>0 (pada gambar baris ketiga). 

Diperoleh luas daerah tersebut adalah penjumlahan luas daerah antara Z=0 hingga Z=0,2 dengan luas daerah antara Z=-0,4 hingga Z=0.

Luas daerah Z<-0,4 akan sama dengan luas daerah Z>0,4 (simetris).

Contoh 5:

Caranya :

Cerminkan kuva Z<-1,25 terhadap kurva Z>0 sehingga memiliki nilai sama dengan Z>1,25.
Nah untuk menghitungnya sama dengan contoh 2.

2. Tabel Distribusi Z Model 2 

Tabel model 2 di atas berbeda dengan yang Model 1 dimana luas daerahnya pada Z>0, sedangkan model 2 adalah luas daerah pada -¥<Z<z baik z>0 atau pun z<0. Angka pada kolom paling kiri dan angka pada baris paling atas adalah Nilai Z=z serta angka yang ada dalam tabel adalah luas daerah di bawah kurva normal Z.

Contoh 1 :

Contoh 2 :

Contoh 3 :

Contoh 4 :

Selamat Mencoba Untuk Nilai Z lainnya...

Apapun tabel Z yang digunakan harus menghasilkan nilai akhir yang sama.

^_^

Read More

CONTOH TWO WAY ANOVA DENGAN MENGGUNAKAN IBM SPSS 21

Sebelumnya kita sudah berikan contoh mengenai ANOVA dua jalur. 

Nah berikutnya kita coba analisa menggunakan IBM SPSS 21 dengan data yang baru. 

Apakah ada pengaruh pemberian kupon dan promosi pada penjualan suatu produk di perusahaan ABC?

Berikut datanya :

Data Penjualan

Berikut langkah-langkahnya :

1. Buka IBM SPSS 21.

2. Definisikan variabel pada Variable View seperti di bawah ini.

 3. Bagian kolom Value untuk baris 2 promosi, isikan data berikut

4. Bagian kolom Value untuk baris 3 Kupon, isikan data berikut 

 5. Pada Data View isikan data seperti di bawah ini

Artinya : pada baris ke-17, kepuasan bernilai 4 dengan promosi yang gencar dan tidak ada kupon.

Dan pada baris ke-22, kepuasan bernilai 7 dengan promosi yang gencar dan ada kupon, dst.

6. Klik Analyze -> General Linear Model -> Univariate 

7. Pada tabel Univariate pindahkan variabel Efisiensi Pemakaian BBM pada Dependent Variable dan variabel Merek Mobil lalu klik OK

8. Diperoleh Output sebagai berikut

Pada tabel Between-Subject Factor menunjukkan jumlah data yang diproses dan masing-masing kategori diberikan informasi jumlah datanya.

Pada tabel Tests of Between-Subject Effects merupakan hasil yang akan dianalisa yaitu 

1. Uji Mean Kepuasan berdasarkan Promosi

a. Variabel Promosi

Hipotesa Uji :

Ho : Rata-rata kepuasan antara promosi tidak gencar, gencar dan sangat gencar adalah sama.

Ha : Rata-rata kepuasan antara promosi tidak gencar, gencar dan sangat gencar adalah beda.

Statistik Uji :

Pilih nilai signifikansi 5%.

Keputusan :

Dari tabel kedua output pada kolom Sig. diperoleh nilai Sig.=0,000 untuk variabel promosi. Karena nilai Sig.=0,000 < 0,05, sehingga Ho ditolak dan Ha diterima.

Kesimpulan :

Terdapat perbedaan rata-rata kepuasan antara promosi tidak gencar, gencar dan sangat gencar.

b. Variabel Kupon

Hipotesa Uji :

Ho : Rata-rata kepuasan antara diberi kupon dengan tidak adalah sama.

Ha : Rata-rata kepuasan antara diberi kupon dengan tidak adalah beda.

Statistik Uji :

Pilih nilai signifikansi 5%.

Keputusan :

Dari tabel kedua output pada kolom Sig. diperoleh nilai Sig.=0,000 untuk variabel kupon. Karena nilai Sig.=0,000 < 0,05, sehingga Ho ditolak dan Ha diterima.

Kesimpulan :

Terdapat perbedaan rata-rata kepuasan antara diberikan kupon dengan tidak.

2. Uji interaksi

Hipotesis Uji :

Ho : Tidak terdapat interaksi antara variabel kupon dengan variabel promosi

Ha : Terdapat interaksi antara variabel kupon dengan variabel promosi.

Statistik Uji :

Pilih nilai signifikansi 5%.

Keputusan :

Dari tabel kedua output pada kolom Sig.=0,206 untuk variabel interaksi antara kupon dan promosi. Karena nilai Sig.=0,206 > 0,05, sehingga Ho diterima dan Ha ditolak.

Kesimpulan :
Tidak terdapat interaksi antara variabel kupon dengan variabel promosi.

Dari hasil pengujian diatas diperoleh kesimpulan bahwa adanya hubungan positif antara penjualan dengan pemberian kupon dan promosi. Adanya pemberian kupon dapat meningkatkan penjualan begitunya dengan adanya promosi barang dapat meningkatkan penjualan.

Note : Sebelum melakukan TWO-WAY ANOVA, terlebih dahulu melakukan uji asumsi. Jika terpenuhi maka dapat lanjut ke TWO-WAY ANOVA. 

Reference:

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

Download Co-So - Statistik Distribusi Sampling Rataan

Co-So Soal Distribusi Sampling Rataan

Read More

Download C-So - Statistic Teorema Bayes

Co-So Teorema Bayes

Read More