ANALISIS REGRESI LINIER SEDERHANA DENGAN IBM SPSS 21

Dari contoh sebelumnya pada penghitungan manual regresi linier sederhana, maka dapat kita gunakan software statistik IBM SPSS 21 sebagai berikut :

Kasus masih sama,Sebuah penelitian terhadap batang pohon mahoni yang diambil delapan sampel acak dan akan diteliti apakah ada pengaruh diameter batang pohon dengan tinggi batang pohon. 

Langkah-langkah yang dilakukan :

1. Klik Start -> IBM SPSS 21

2. Pada Variable View input data seperti berikut ini :

3. Pada Data View input data seperti berikuti ini :

4. Klik Analyze -> Regression -> Linear

5. Pindahkan Variabel Tinggi Pohon ke kolom Dependent dan Variabel Diameter Batang Pohon ke kolom Independent.

Pada Method pilih Enter berarti analisis data setiap variabel dianalisis satu-satu.

6. Tandai beberapa item :

• Estimates : untuk menentukan konstanta a dan b
• Model Fit: untuk uji ketepatan model regresi linier
• R Squared Change : untuk menentukan nilai R² 

• Klik Continue

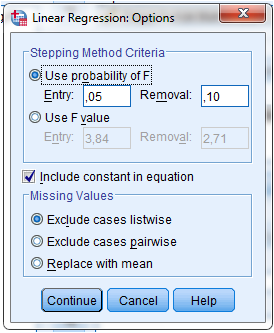
7. Pilih Options masukkan nilai taraf signifikansi dalam hal ini kita pilih 5% sehingga ketik 0,05 pada kolom Entry. Tandai Include Constant in Equation. 

Pada kolom ini brfungsi untuk uji-F, digunakan untuk melihat pengaruh variabel bebas X secara bersamaan terhadap variabel tak bebas Y. (Regresi Linear Berganda)

Pada Missing Values

• Exclude cases listwise :hanya data yang valid untuk semua variabel yang ikut dianalisis
• Exclude cases pairwise :menganalisis koefisien korelasi dan seluruh cases yang berharga valid dari dua variabel yang dikorelasikan.
• Replace with mean : Semua data dianalisis dan untuk data yang kosong digantikan dengan rata-rata variabel tersebut.

Klik Continue

8. Output Analisis Regresi Linear Sederhana

Merupakan output dari method yang kita pilih yaitu Enter.

Dari output di atas diperoleh nilai koefisien determinasi R² = 0,785 berarti sekitar 75,5% variasi dari diameter batang pohon mahoni dapat menjelaskan variasi dari variabel tinggi batang pohon mahoni. (cukup tinggi).

dan nilai korelasi R = 0,886. Artinya hubungan yang kuat antara variabel diameter batang pohon mahoni dengan variabel tinggi pohon mahoni. 

Pada Adjusted R Square diperoleh nilai  0,750 artinya sekitar 75% variasi yang terjadi pada tinggi pohon dapat dijelaskan oleh variabel diameter batang pohon mahoni dan sisanya dijelaskan oleh variabel lainnya.

Note : 

R Square dan Adjusted R Square sama-sama boleh digunakan bedanya adalah jika kita ingin menggeneralisasikan ke populasi maka gunakan Adjusted R Square,dan individu yang kita gunakan adalah dipilih secara acak, namun jika individu atau sampel non acak sebaiknya gunakan R Square. Pada ukuran sampel yang besar, nilai R Square dan Adjusted R Square akan mendekati nilai sama.

Pada kolom B adalah nilai konstanta dan koefisien persamaan regresi. Sehingga dari angka inilah kita dapat membentuk persamaan regresi.

(Constant) = -1,315

Diameter Batang Pohon Mahoni = 4,541

Jadi persamaan regresi yang diperoleh adalah :

Y' = -1,315 + 4,541 X

Dan untuk uji-t diambil dari kolom t dan sid pada variabel Diameter Batang Pohon Mahoni.

Hipotesis Uji :

Ho : b = 0

Ha : b ≠ 0

Taraf Signifikansi :

Pilih nilai a = 5%

Daerah Kritis :

Dengan nilai signifikansi 5% dan derajat bebas 6 maka diperoleh t-tabel = 2,447.

Statistik Uji :

Diperoleh t-hitung = 4,686 dan nilai p-value = 0,003

Keputusan :

Nilai t-hitung = 4,686 > t-tabel = 2,447 atau nilai p-value = 0,003 < 0,05.

Jadi Ho ditolak dan Ha diterima.

Kesimpulan :

Dengan signifikansi 5% diameter batang pohon mahoni berpengaruh terhadap tinggi pohon mahoni.

Note : 

Uji F pada regresi linear sederhana memberikan nilai signifikans yang sama dengan uji t, yaitu sebesar 0,03.

Namun pada regresi linear berganda akan berbeda. 

by MEYF

Read More

CONTOH PENGHITUNGAN MANUAL ANALISIS REGRESI SEDERHANA

Sebuah penelitian terhadap pohon Mahoni, dimana akan diteliti apakah ada hubungan antara tinggi pohon dengan diameter batang pohon, dengan artian apakah ada pengaruh diameter batang pohon terhadap tinggi pohon tersebut.

Diambil sampel secara acak sejumlah delapan pohon mahoni.Dapat dilihat dari Tabel 1 pada kolom X dan Y.

Hal pertama yang akan kita lakukan adalah membentuk persamaan regresi, yaitu :

Y' = a + bX

Selanjutnya adalah menentukan konstanta a dan koefisien b, kita ikuti langkah sebagai berikut :

maka diperoleh :

Persamaan regresi diperoleh :

Y' = -1,3147 + 4,5413X

dimana :

Y' = Tinggi pohon mahoni yang diprediksi

X  = Diameter batang pohon mahoni

Interpretasi dari koefisien regresi :

• Nilai a = -1,3147 artinya tidak ada diameter batang pohon maka tidak ada tinggi pohon. (karena tidak ada tinggi yang bernilai negatif sehingga dianggap nol).
• Nilai b = 4,5413 artinya jika terjadi peningkatan diameter batang pohon mahoni satu satuan maka akan terjadi peningkatan tinggi pohon mahoni sebesar 4,5413 satuan.

Koefisien Determinasi R^{2 :}

r = 0,886 bernilai positif dan kuat

artinya terdapat hubungan atau korelasi yang kuat antara tinggi pohon mahoni dengan diameter batang pohon mahoni. Semakin besar diameter batang pohon mahoni maka semakin tinggi batang pohon mahoni.

R² = 0,886² = 0,785

artinya sekitar 78,5% variasi dari variabel diameter batang pohon mahoni dapat menjelaskan variasi dari variabel tinggi pohon mahoni.

(cukup tinggi)

Standar Error Estimate Persamaan Regresi:

Jadi besarnya standar error estimate persamaan regresi adalah 6,6364. Hal ini menunjukkan penyimpangan data-data terhadap garis regresi, atau bagaimana penyimpangan data yang menyebar disekitar garis regresi.

(cukup kecil).

Pengujian Koefisien Regresi :

> Hipotesis Uji

Ho : b =  0

Ha : b ≠ 0

> Taraf Signifikansi

Pilih nilai signifikansi a = 5%

> Daerah Kritis

dengan nilai a = 5% dan derajat bebas n-2=8-2=6, maka diperoleh nilai t-tabel pada 5%/2 = 2,5% yaitu 2,447.

> Statistik Uji

> Keputusan

nilai t-hitung = 4,6805 > t-tabel = 2,447 sehingga Ho ditolak dan Ha diterima.

> Kesimpulan

Dengan tingkat signifikansi 5% cukup menjelaskan bahwa ada pengaruh diameter batang pohon mahoni terhadap tinggi pohon mahoni.

by MEYF

Reference:

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

-Supranto, J. 2004. Analisis Multivariat : Arti dan Interpretasi. Rineka Cipta. Jakarta.

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

ANALISIS REGRESI SEDERHANA

Dalam analisis regresi sederhana tujuannya adalah untuk melihat hubungan linier antara variabel bebas X dengan variabel tidak bebas Y dan memprediksi nilai variabel tidak bebas Y dari nilai yang diberikan variabel bebas X.

Asumsi-asumsi dasar yang harus dipenuhi sebelum melakukan analisis regresi linier sederhana adalah :

1. Model regresi harus linier secara parameter (uji liniearitas). 
2. Berdistribusi normal (uji normalitas).
3. Varians data sama (uji homogenitas).

Asumsi klasik regresi :

1. Tidak ada korelasi antara variabel bebas atau hubungan linier sempurna (uji multikolinearitas)
2. Varians masing-masing error selalu konstan (uji heteroskedasitas).
3. Tidak ada korelasi antara error yang satu dengan error yang lainnya (uji autokorelasi).
4. Masing-masing error berdistribusi normal dengan mean nol dan standar deviasi tetap.

Dalam analisis regresi yang harus diketahui adalah :

> Variabel bebas / independent / tidak terikat

• Biasanya disimbolkan dengan X (huruf kapital).Adalah variabel yang mempengaruhi variabel lain.(pls see this jenis-jenis variabel).

> Variabel tidak bebas / dependent / terikat

• Biasanya disimbolkan dengan Y (huruf kapital).Adalah variabel yang dipengaruhi oleh variabel lain.(pls see this jenis-jenis variabel).

> Persamaan Regresi : Y' = a + bX 

• Dimana : 
• Y' = variabel tidak bebas (nilai yang diprediksikan)
• X  = Variabel bebas (nilai yang memprediksi / prediktor)
• a  = Konstanta (jika nilai X = 0, maka Y' = a)
• b  = Koefisien regresi 

Dalam analisis regresi linier sederhana adalah menentukan nilai konstanta a dan koefisien b. Apakah koefisien b bernilai positif atau negatif, apakah koefisien b bernilai nol atau tidak. Jika 

• b = 0, berarti tidak ada pengaruh antara variabel bebas X terhadap variabel tidak bebas Y.
• b < 0, berarti hubungan yang berbalik arah antara variabel bebas X dengan variabel tak bebas Y.
• b > 0, berarti hubungan yang searah antara variabel bebas X dengan variabel tak bebas Y.

Menghitung koefisien a dan b :

> Analisis Koefisien Determinasi R²

• Artinya : Sekitar R² variasi variabel tidak bebas Y dapat dijelaskan oleh variabel bebas X.
• Koefisien determinasi digunakan untuk mengetahui prosentase sumbangan pengaruh variabel bebas X terhadap variabel bebas Y.
• Jika nilai R²=0 berarti variasi variabel bebas X tidak sedikitpun dapat menjelaskan variasi variabel tidak bebas Y dalam model tersebut.
• Jika nilai R²=1 berarti variasi variabel bebas X dapat menjelaskan dengan SEMPURNA variabel tidak bebas Y dalam model tersebut. 
• Jadi nilai koefisien determinasi R² sebesar mungkin.

> Standar Error Estimate

• Nilai Y' adalah nilai prediksi sehingga terjadi kesalahan/galat/error dalam memprediksinya. Standar error digunakan untuk mengukur simpangan data aktual di sekitar garis regresi. 
• Jadi nilai standar error estimate harus sekecil mungkin 

> Uji Koefisien Regresi Sederhana (Uji - t)

• Tujuan untuk mengetahui apakah variabel bebas X berpengaruh secara signifikan terhadap variabel tidak bebas Y.(Signifikan berarti dapat digeneralisasikan).

Langkah-langkah pengujiannya:

1.  Menentukan Hipotesis Uji

H_o : b = 0 

    (tidak ada pengaruh antara variabel bebas X terhadap variabel tidak bebas Y)

H_a : b ≠ 0 

    (ada pengaruh antara variabel bebas X terhadap variabel tidak bebas Y)

2.  Menentukan Tingkat Signifikansi

Tingkat signifikansi yang biasa digunakan adalah 5%, adapun yang lainnya adalah 1% - 10%.

3.  Menentukan Daerah Penolakan H_o (Daerah Kritis)

Bentuk pengujian kita adalah dua arah sehingga gunakan uji-t dua arah :

H_o akan ditolak jika t_hitung > t_tabel atau -(t_hitung) < -(t_tabel),berarti H₁ diterima.

H_o akan diterima jika -(t_hitung) < t_tabel < t_hitung , berarti H₁ ditolak.

4.  Menentukan t-hitung

5.  Keputusan (Membandingkan t-hitung dengan t-tabel.

6. Kesimpulan (Apakah ada pengaruh antara variabel bebas X terhadap variabel tidak bebas Y).

by MEYF

Reference:

- Mendenhall, Sincinch. 1996. A Second Course In Statistics. Regression Analysis. Fifth Edition. Prentice Hall Internatiomal Edition. 

- Priyatno, Duwi. 2010. Paham Analisa Statistik Data dengan SPSS. Mediakom. Yogyakarta.

- Sugiyono. 2008. Metode Penelitian Bisnis. Alfabeta. Bandung.

- Sugiyono. 2009. Metode Penelitian Kuantitatif Kualitatif dan R & B. Bandung.

- Sugiyono, 2008. Statistik Nonparametris untuk Penelitian. Alfabeta. Bandung.

-Supranto, J. 2004. Analisis Multivariat : Arti dan Interpretasi. Rineka Cipta. Jakarta.

-Walpole, Ronald E. 1992. Pengantar Statistika Edisi ke-3. PT Gramedia Pustaka Utama. Jakarta.

Read More

PENGUJIAN HIPOTESIS

Pengujian Hipotesis

Read More

HOW TO LEARN MATHEMATIC?

Mathematic is the door and the key of science, every we run then we meet mathematic, although we learn about social science we never far away from it. Since kid we have been taught about mathematic, we knew numbers and add numbers by using fingers. Do you realize that you always right using mathematic when you count your money. And, you always right using mathematic when you count your mark test.

Somepeople thinks “Math is Mental Abuse To Humans” because they don't find the beauty on it. Math is like horror and ghost that make them scare to learn it. They try to far away and don't want to know more about mathematic. But don't you realize that mathematic is look like art and poetry with more beautiful number and symbol. The piano and other instruments can be played if we can play with the numbers that can give nice melody. The algebra, calculus, geometry, statistic, etc. are kind of instrument in our mind that can play the numbers and give the beautiful result when we use it properly. When we proof some formula, mathematic is look like poetry, it is full with symbol and mathematics statement that it has the meaning on it.

How beautiful mathematics, first time you know mathematics make you are curious and you want to solve it properly. When you curious and you learn it, you curious again then you learn it again, you will do continue like this, then it makes you know how beautiful mathematics is. Mathematic will come to close with you if you are not afraid or far from it. For the first time you should try to solve mathematic problems, and you can do it then make you want to try to solve new mathematic problem, and you do it again and again.

The point of to love math is practice..practice..practice... and practice. Never boring with that activity. Then, when you can solve mathematic problem then make you want to know your next ability to solve it again. You will continue and this makes your mind will always remember about math. Like you love someone, when you love her/him, you always remember her/him, then you always want to know about her/him. You want to know her/his feeling and you want to try to keep contact and give more attention to her/him. It is the same with math, when you give full attention on it, you will know mathematic well, then mathematic will give good feedback to you then you love it.

How lucky you are when you find the beauty on mathematic, you will do like mathematicians that always think positive to solve their problems, think creative, think simplicity, do honest, think positive and never give up about their dream and their life. When you love mathematic, you will know that God is so great that has create mathematic for us. Then you try to find and solve a riddle or fun of mathematic because most people love fun and happy condition. So when you find it on mathematic, you will like it.

This is the simple steps how to learn mathematic, do more practice, Love mathematic and know riddle or fun mathematic. And, you will find the change on your mind.

For me, first time I know mathematic since kid, and in elementary school, my teacher always taught me mathematic every day in a class. Then, she gave me more homework so I always practiced on it. Then, my teacher gave me more riddle and fun story about mathematic. Bside thay my parents knew my ability in this subject. They asked me to learn mathematic in university. I did it with feeling love on mathematic.

And for you that still learn mathematic, don’t be scare if you cannot solve mathematic problem, it mean that God gives you a chance to be  creative people, because you will think creative to solve it. God gives you a chance to be a people who never give up because you will try to solve it properly. God give you a chance to be a simple human to think and face problems because you will try simple solution to solve it. God give you chance to think positive because you will be positive that you are abble to solve it. God give you chance to be honest, because mathematic is an exact science and it has certainty result that could not be annoyed. God give you chance to know Him, because from mathematic we know one of knowledge that God give to us. This is a foundation and this is a base or key of other science. Only one subject that act like this, it is mathematic.

How beautiful mathematic is. And we should proud to learn and to know more about mathematic. Let’s change your mind to love mathematic.

By : MEYF

^_^

Read More

PENGENALAN SOFTWARE STATISTIKA

Dalam memudahkan kita mengolah data dengan analisa statistika, kita dapat menggunakan berbagai macam alat bantu atau software. Adapun software statistika yang dapat digunakan sangatlah banyak namun tidak semuanya memiliki keakuratan yang baik. Ada beberapa software statistika yang sering digunakan baik dalam dunia pendidikan atau pun pekerjaan. 

1. SPSS

Tentu Anda sering mendengar program statistika satu ini, di perkuliahan atau pun di beberapa perusahaan besar pun menggunakan software statistika ini. SPSS singkatan dari Statistical Package for the Social Software. Pertama kali dirilis pada tahun 1968 yang dikembangkan oleh Norman H. Nie dan C. Hadlai Hull. 

SPSS pertama kalo muncul dengan versi PC dengan nama SPSS/PC+ (versi DOS). Setelah mulai populernya sistem WINDOWS maka SPSS berkembang mulai dari versi 6.0 hingga sekarang. SPSS pada awalnya dibuat untuk keperluan pengolahan data statistik untuk ilmu-ilmu sosial (sesuai dengan singkatan dari SPSS itu sendiri).

SPSS pada tanggal 28 Juli 2009 disebut sebagai PASW (Predictive Analytics SoftWare), karena perusahaan ini telah dibeli oleh perusahaan IBM dengan harga US$ 1,2 milyar. Dan pada Januari 2010 menjadi SPSS : Sebuah Perusahaan IBM", dan menjadi nama IBM SPSS yang sepenuhnya diintegrasikan ke dalam IBM Corporation dan merupakan salah satu merk dibawah IBM Software Group Portofolio Bisnis Analytics bersama dengan IBM Cognos.

Adapun IBM SPSS dapat mengolah data :

1. Statistika Dasar: Descriptives Statistics : Cross tabulation, Frequencies, Descriptives, Explore, Descriptive Ratio Statistics.

2. Bivariate Statistics : Means, t-test, ANOVA, Correlation (bivariate, partial, distances), Nonparametric tests

3. Prediction for numerical outcomes : Linear Regression

4. Prediction for identifying groups : Factor analysis, cluster analysis, Discriminant analysis.

Ada beberapa keunggulan diantaranya, yaitu :

1. SPSS dapat membaca dan menulis data dari ASCII file teks, paket statistik lainnya, spreadsheet dan database. 

2. SPSS dapat membaca dan menulis ke eksternal tabel database relasional melalui ODBC dan SQL.

3. Output statistiknya adalah sebuah format file proprietary (*.SPV file, mendukung tabel pivot). Output dapat diekspor ke teks, atau microsoft word.

4. Memberikan informasi yang lebih akurat dengan memperlakukan missing data secara tepat

(Sumber : http://en.wikipedia.org/wiki/SPSS).

2. MINITAB

Software statistika berikutnya adalah MINITAB yaitu program komputer yang dirancang untuk melakukan pengolahan statistik. Minitab menggabungkan kemudahan penggunaan layaknya Microsoft Excel dengan kemampuannya melakukan analisis statistik yang kompleks. 

Minitab dikembangkan di Pennsylvania State University oleh periset Barbara F. Ryan, Thomas A. Ryan, Jr., dan Brian L. Joiner pada tahun 1972. Minitab didistribusikan oleh Minitab Inc, sebuah perusahaan swasta yang bermarkas di State College, Pensylvania dengan kantor cabang Coventry, Inggris (Minitab Ltd) Paris, Perancis (Minitab SARL) dan Sydney, Australia (Minitab Pty.).

Minitab seringkali digunakan dalam perusahaan industri sebagai implementasi Six Sigma - TQM, CMMI serta metode perbaikan proses yang berbasis statistik lainnya dikenal dengan Design of Experiment (DOE). Minitab Inc, juga membuat perangkat lunak sebagai pelengkap Minitab 16, Quality Trainer dan Quality Companion 3.

Adapun analisis data yang dapat dilakukan oleh Minitab diantaranya :

1. Mengelola data dan file - spreadsheet untuk analisis data yang lebih baik.

2. Analisis Regresi.

3. Power dan ukuran sampel.

4. Tabel dan grafik.

5. Analisis Multivariate : Factor analysis, Cluster analysis, Correspondence analysis, dll.

6. Nonparametric Test : Sign Test, Run Test, Friedmann Test, dll.

7. Time Series dan Forecasting : Time series plot, exponential smoothing, trend analysis.

8. Statistical Process Control (SPC)

9. Analisis sistem pengukuran (measurement).

10. ANOVA, dll

Adapun keunggulan MINITAB dari segi aplikasi adalah 

1. Menyediakan StatGuide sebagai panduan dalam mengolah dan interpretasi data 

2. Ukuran worksheet yang dapat memuat kolom sampai 4000 kolom.

3. Memiliki dua layar primer yaitu Worksheet dan Sesi Command. 

4. Tampilan Menu di Minitab lebih lengkap disertai toolbar yang lebih memudahkan dalam menjalankannya.

5. Mempunyai file Minitab Worksheet (MTW) dan Minitab Project (MPJ) yang digunakan untuk membedakan file worksheet dan file project.

6. Minitab menyediakan ReportPad agar mudah membuat laporan project yang telah dibuat.

7. Menyediakan fasilitas makro untuk membuat program yang berulangkali dipakai, memperluas fungsi Minitab, dan mendesain perintah sendiri, dan bahasa pemograman makro yang lebih mudah.

8. File dapat disimpan dalam nama yang panjang.

Read More